Kako pronaći osnovu jezgre matrice. Formiranje matrice cjelovite slike s odvojenom percepcijom elemenata složenog objekta. Odrednice. Izračunavanje determinanti

Pojašnjenje principa integracije diskretnih informacija tijekom odvojene percepcije elemenata složenog objekta hitan je interdisciplinarni problem. U članku se govori o procesu konstruiranja slike objekta, koji je kompleks blokova, od kojih svaki kombinira skup malih elemenata. Kao predmet proučavanja odabrana je konfliktna situacija, budući da je dosljedno bila u polju pozornosti s konstantnom strategijom analize informacija. Okolnosti situacije bile su komponente objekta i zasebno su percipirane kao prototipovi sukoba. Zadatak ovog rada bio je matematički izraziti matricu koja odražava sliku problematične situacije ponašanja. Rješenje problema temeljilo se na podacima iz vizualne analize oblikovanja grafičke kompozicije čiji su elementi odgovarali situacijskim okolnostima. Veličina i grafička obilježja odabranih elemenata, kao i njihov raspored u kompoziciji, poslužili su kao orijentir za prepoznavanje redaka i stupaca u slikovnoj matrici. Studija je pokazala da je dizajn matrice određen, prvo, motivacijom ponašanja, drugo, uzročno-posljedičnim odnosima situacijskih elemenata i slijedom dobivanja informacija, te također, treće, odabirom dijelova informacija u skladu s njihovim težinskim parametrima. Može se pretpostaviti da su spomenuti matrični vektorski principi oblikovanja slike situacije ponašanja karakteristični za konstruiranje slika i drugih objekata na koje se usmjerava pozornost.

vizualizacija

percepcija

diskretnost informacija

1. Anohin P.K. Ogledi o fiziologiji funkcionalnih sustava. – M.: Medicina, 1985. – 444 str.

2. Ilyin V. A., Poznyak E. G. Linearna algebra: udžbenik za sveučilišta. – 6. izd. – M.: Fizmatlit, 2004. -280 str.

3. Lavrov V.V. Mozak i psiha. – St. Petersburg: RGPU, 1996. – 156 str.

4. Lavrov V.V., Lavrova N.M. Utjecaj agresije na cjelovitost, cjelovitost, vrijednost i subjektivnost slike konfliktne situacije // Kognitivna psihologija: interdisciplinarna istraživanja i integrativne prakse. – St. Petersburg: VVM, 2015. – P. 342-347.

5. Lavrov V.V., Rudinski A.V. Trijada strategija obrade informacija pri prepoznavanju nepotpunih vizualnih slika // Fundamentalna istraživanja. – 2014. – broj 6 (2). – str. 375-380.

6. Lavrova N.M., Lavrov V.V., Lavrov N.V. Medijacija: donošenje odgovornih odluka. – M: OPPL, 2013. – 224 str.

7. Shelepin Yu.E., Chikhman V.N., Foreman N. Analiza studija percepcije fragmentiranih slika - holistička percepcija i percepcija na temelju informativnih značajki // Russian Physiological Journal. 2008. – T. 94. br. 7. – P. 758-776.

Rezultati istraživanja percepcije nepotpunih slika proširili su perspektivu proučavanja principa koji određuju integraciju diskretnih informacija i montažu cjelovitih slika. Analiza značajki prepoznavanja fragmentiranih slika kada se prezentiraju s promjenjivim brojem fragmenata omogućila je praćenje triju strategija za konstruiranje cjelovite slike u uvjetima nedostatka informacija. Strategije su se razlikovale u procjeni značaja dostupnih informacija za formiranje koherentne slike. Drugim riječima, svaku strategiju karakterizirala je manipulacija parametrima težine dostupnih informacija. Prva strategija predviđala je ekvivalentnost fragmenata slike - njegova identifikacija je provedena nakon akumulacije informacija do razine dovoljne za potpuno razumijevanje prikazanog objekta. Druga se strategija temeljila na diferenciranom pristupu ocjenjivanju težine dostupnih informacija. Ocjena je dana u skladu s postavljenom hipotezom o suštini predmeta. Treća strategija određena je motivacijom da se maksimalno iskoriste dostupne informacije, kojima se pridavala velika težina i smatrala se znakom ili prototipom stvarnog objekta. Važna točka u dosadašnjem radu bilo je razmatranje moždanih mehanizama koji osiguravaju promjenu strategija ovisno o dominantnoj emociji i motivaciji ponašanja. To se odnosi na nespecifične moždane sustave i heterogenost neuronskih modula koji rade pod kontrolom središnje kontrole. Provedena istraživanja, kao i ona poznata iz literarnih izvora, ostavila su otvorenim pitanje principa distribucije informacija u cjelovitoj slici. Za odgovor na postavljeno pitanje bilo je potrebno promatrati formiranje slike predmeta na koji je pozornost bila usmjerena dulje vrijeme, a odabrana strategija konstruiranja slike ostaje nepromijenjena. Kao takav objekt mogla bi poslužiti konfliktna situacija, budući da je dosljedno bila u polju pozornosti, a druga strategija analize okolnosti ostala je konstantna. Zavađene strane su odbacile prvu strategiju zbog produljenja trajanja sukoba, a nisu primijenile treću strategiju, izbjegavajući pogrešne odluke.

Cilj Ovaj rad je trebao razjasniti principe konstruiranja slikovne matrice na temelju elemenata informacija dobivenih odvojenom percepcijom komponenti složenog objekta na koji je usmjerena pozornost. Riješili smo sljedeće probleme: prvo, odabrali smo objekt na koji je pažnja bila usredotočena dugo vremena, drugo, metodom vizualizacije slike pratili smo fragmentaciju informacija dobivenih tijekom percepcije objekta, a zatim, treće, formulirati principe integralne distribucije fragmenata u matrici.

Materijali i metode istraživanja

Problematična bihevioralna situacija poslužila je kao višekomponentni objekt koji je bio stabilno u polju pažnje s nepromijenjenom strategijom analize dostupnih informacija. Problem je nastao zbog sukoba u odnosima između članova obitelji, kao i zaposlenika industrijskih i obrazovnih ustanova. Pokusi u kojima se analizirala slika situacije prethodili su medijaciji koja je imala za cilj rješavanje proturječja između zavađenih strana. Prije početka medijacijskih pregovora, predstavnici stranaka u sporu dobili su ponudu da kao subjekti sudjeluju u eksperimentima koristeći tehniku ​​koja olakšava analizu situacije. Tehnika vizualizacije uključivala je konstrukciju grafičke kompozicije koja odražava konstrukciju slike koja je nastala tijekom zasebne percepcije komponenti složenog objekta. Tehnika je služila kao alat za proučavanje procesa oblikovanja cjelovite slike iz skupa elemenata koji odgovaraju detaljima predmeta. Skupinu ispitanika činilo je 19 žena i 8 muškaraca u dobi od 28 do 65 godina. Da bi se dobila cjelovita vizualna slika situacije, od ispitanika se tražilo da izvrše sljedeće radnje: 1) obnoviti u svom sjećanju okolnosti konfliktne situacije - događaje, odnose s ljudima, motive vlastitog ponašanja i onih oko njih; 2) procijeniti okolnosti prema njihovom značaju za razumijevanje biti situacije; 3) podijeliti okolnosti na povoljne i nepovoljne za rješavanje sukoba i pokušati pratiti njihov odnos; 4) odaberite, po vašem mišljenju, odgovarajući grafički element (krug, kvadrat, trokut, crta ili točka) za svaku od okolnosti koje karakteriziraju situaciju; 5) oblikovati kompoziciju od grafičkih elemenata, vodeći računa o značaju i odnosu okolnosti koje ti elementi prenose, te tako dobivenu kompoziciju nacrtati na papiru. Analizirane su grafičke kompozicije – procijenjena je uređenost i omjer veličina slikovnih elemenata. Nasumične, nesređene kompozicije su odbačene, a ispitanici su zamoljeni da preispitaju međuodnos situacijskih okolnosti. Rezultati generalizirane analize kompozicije poslužili su kao smjernica za formuliranje matematičkog izraza matrice slike.

Rezultati istraživanja i rasprava

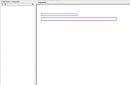
Svaka grafička kompozicija kroz koju je subjekt predstavljao konstrukciju slike situacije ponašanja bila je originalna. Primjeri sastava ilustrirani su na slici.

Grafičke kompozicije koje odražavaju slike problematičnih situacija ponašanja u kojima su se subjekti nalazili (svaki element kompozicije odgovara situacijskim okolnostima)

Jedinstvenost kompozicija svjedoči o odgovornom pristupu ispitanika analizi situacija, uzimajući u obzir njihove posebnosti. Broj elemenata u kompoziciji i dimenzija elemenata, kao i oblikovanje kompozicije, odražavali su procjenu spleta okolnosti.

Nakon što je uočena originalnost kompozicija, studija se okrenula identificiranju temeljnih značajki dizajna slike. U nastojanju da se izgradi cjelovita kompozicija koja odražava sliku situacije, ispitanici su rasporedili elemente u skladu sa svojim individualnim preferencijama, kao i uzimajući u obzir uzročno-posljedične odnose okolnosti i splet okolnosti tijekom vremena. Sedam ispitanika radije je postavilo kompoziciju u obliku crteža, čija je konstrukcija određena unaprijed nacrtanim figurativnim planom. Na sl. 1 (a, b, d) daje primjere takvih sastava. Prije izrade kompozicije, dvoje ispitanika je svjesno odabralo ideju koja je bila temelj plana, a pet intuitivno, bez davanja logičnog objašnjenja zašto su se odlučili na odabranu opciju. Preostalih dvadeset ispitanika izradilo je shematski sastav, obraćajući pozornost samo na uzročno-posljedične odnose okolnosti i splet okolnosti tijekom vremena (slika 1, c, e, f). U skladbi su spojene srodne i slučajne okolnosti. Eksperimenti nisu tumačili bit sukoba pomoću podataka o grafičkoj kompoziciji. Ovo tumačenje je naknadno provedeno u okviru medijacije, kada se utvrđivala spremnost stranaka na pregovore.

Analiza kompozicija omogućila je praćenje ne samo razlike, već i univerzalnosti načela oblikovanja slike situacije. Prvo, kompozicije su se sastojale od grafičkih elemenata, od kojih je svaki odražavao okolnosti koje su imale zajedništvo. Zajedničkost okolnosti nastala je zbog uzročno-posljedičnih i vremenskih odnosa. Drugo, okolnosti su bile od nejednake važnosti za razumijevanje suštine problemske situacije. Odnosno, okolnosti su se razlikovale u parametrima težine. Visoko značajne okolnosti prikazane su grafičkim elementima u povećanoj veličini u odnosu na manje značajne. Uočene značajke slike uzete su u obzir prilikom sastavljanja matrice slike. To znači da su veličina i grafička obilježja odabranih elemenata, kao i njihov prostorni položaj u grafičkoj kompoziciji, poslužili kao vodilja za konstrukciju informacijske matrice koja je odražavala sliku situacije i bila njezin matematički model. Pravokutna matrica, predstavljena kao tablica, podijeljena je na retke i stupce. U odnosu na sliku problemske situacije koja se formira, u matrici su identificirani retci koji su sadržavali težinske elemente prototipova, objedinjene uzročno-posljedičnim i vremenskim vezama, te stupce koji sadrže elementarne podatke koji se razlikuju po težinskim parametrima.

(1)

Svaka pojedina linija odražavala je formiranje dijela slike ili, drugim riječima, prototipa predmeta. Što je više linija i što je veće m, to je objekt percipiran cjelovitije, budući da su strukturalna i funkcionalna svojstva koja su mu poslužila kao prototipovi potpunije uzeta u obzir. Broj stupaca n određen je brojem detalja zabilježenih prilikom konstruiranja prototipa. Može se pretpostaviti da što je više fragmenata informacija velike i male težine akumulirano, to je prototip potpunije odgovarao stvarnosti. Matricu (1) karakterizirala je dinamičnost, jer se njezina dimenzija mijenjala u skladu s cjelovitošću slike opažanog objekta.

Ovdje je prikladno napomenuti da cjelovitost nije jedini pokazatelj kvalitete slike. Slike predstavljene na umjetničkim platnima često su inferiorne fotografijama u pogledu detalja i korespondencije sa stvarnošću, ali istovremeno mogu biti superiorne u povezivanju s drugim slikama, u poticanju mašte i izazivanju emocija. Navedena primjedba pomaže razumjeti značaj parametara amn, koji označavaju težinu fragmenata informacija. Debljanje je nadoknadilo nedostatak dostupnih podataka. Kako je pokazalo istraživanje strategija prevladavanja neizvjesnosti, prepoznavanje velikog značaja dostupnih informacija ubrzalo je donošenje odluka u problemskoj situaciji.

Dakle, proces formiranja cjelovite slike možemo protumačiti ako ga povežemo s manipulacijom informacijama unutar matrice. Manipulacija se izražava voljnom ili nevoljnom (svjesnom, svrhovitom ili intuitivno nesvjesnom) promjenom težinskih parametara informacijskih fragmenata, odnosno promjenom vrijednosti amn. U tom se slučaju povećava ili smanjuje vrijednost bm, koja karakterizira značaj prototipa, a istodobno se mijenja rezultirajuća slika br. Ako se okrenemo matričnom modelu formiranja slike, koji pokriva skup podataka o objektu, tada je organizacija slike opisana na sljedeći način. Označimo vektor praslika koji sadrži m komponenti sa

gdje je T znak transpozicije, a svaki element vektora praslike ima oblik:

Tada se izbor rezultirajuće slike može provesti prema Laplaceovom pravilu:

gdje je br konačni rezultat formiranja čvrste slike, koja ima vrijednosti bm kao svoje komponente, amn je skup vrijednosti koje određuju položaj i parametre težine varijable u liniji koja odgovara predslici . U uvjetima ograničenih informacija, konačni rezultat može se povećati povećanjem težine dostupnih podataka.

Na kraju razmatranja izloženog materijala o principima oblikovanja slike, skreće se pozornost na potrebu preciziranja pojma „slika“, budući da u literaturi ne postoji općeprihvaćeno tumačenje. Pojam, prije svega, označava formiranje cjelovitog sustava fragmenata informacija koji odgovaraju detaljima objekta u polju pažnje. Štoviše, veliki detalji objekta odražavaju se podsustavima fragmenata informacija koji čine prototipove. Objekt može biti predmet, pojava, proces, kao i situacija ponašanja. Formiranje slike osigurava se asocijacijama primljenih informacija i onih koje su sadržane u sjećanju i povezane s percipiranim objektom. Konsolidacija fragmenata informacija i asocijacija pri stvaranju slike ostvaruje se u okviru matrice čiji se dizajn i vektor biraju svjesno ili intuitivno. Izbor ovisi o preferencijama postavljenim motivima ponašanja. Ovdje se posebna pažnja posvećuje temeljnoj točki - diskretnosti informacija koje se koriste za sastavljanje cjelovite matrice slike. Cjelovitost, kako je prikazano, osiguravaju nespecifični moždani sustavi koji kontroliraju procese analize primljenih informacija i njihovu integraciju u memoriju. Cjelovitost se može dogoditi pri minimalnim vrijednostima n i m jednakim jedan. Slika dobiva visoku vrijednost zbog povećanja parametara težine dostupnih informacija, a cjelovitost slike se povećava kako se povećavaju vrijednosti n i m (1).

Zaključak

Vizualizacija elemenata slike omogućila je praćenje principa njezinog dizajna u uvjetima odvojene percepcije okolnosti problematične situacije ponašanja. Kao rezultat provedenog rada pokazalo se da se konstrukcija cjelovite slike može smatrati raspodjelom fragmenata informacija u strukturi matrice. Njegov dizajn i vektor određeni su, prvo, motivacijom ponašanja, drugo, uzročno-posljedičnim vezama okolnosti i vremenskim slijedom dobivanja informacija, i treće, odabirom informacija u skladu s njihovim težinskim parametrima. Cjelovitost matrice slike osigurana je integracijom diskretnih informacija koje odražavaju percipirani objekt. Nespecifični moždani sustavi čine mehanizam odgovoran za integraciju informacija u koherentnu sliku. Pojašnjenje matričnih principa formiranja slike složenog objekta proširuje perspektivu razumijevanja prirode ne samo cjelovitosti, već i drugih svojstava slike. To se odnosi na cjelovitost i sigurnost slikovnog sustava, kao i na vrijednost i subjektivnost uzrokovanu nedostatkom cjelovite informacije o objektu.

Bibliografska poveznica

Definicija 1. Slika linearnog operatora A je skup svih elemenata koji se mogu predstaviti u obliku , gdje je .

Slika linearnog operatora A je linearni podprostor prostora. Njegova dimenzija se zove rang operatera A.

Definicija 2. Jezgra linearnog operatora A je skup svih vektora za koje .

Jezgra je linearni podprostor prostora X. Njegova dimenzija se zove kvar operatera A.

Ako operator A djeluje u -dimenzionalnom prostoru X, tada vrijedi sljedeća relacija + =.

Poziva se operator A nedegeneriran, ako je njegova jezgra . Rang nedegeneriranog operatora jednak je dimenziji prostora X.

Neka je matrica linearne transformacije A prostora X u nekoj bazi, tada su koordinate slike i inverzne slike povezane relacijom

Dakle, koordinate bilo kojeg vektora zadovoljavaju sustav jednadžbi

Iz toga slijedi da je jezgra linearnog operatora linearna ljuska temeljnog sustava rješenja danog sustava.

Zadaci

1. Dokažite da je rang operatora jednak rangu njegove matrice u proizvoljnoj bazi.

Izračunajte jezgre linearnih operatora definiranih u određenoj bazi prostora X pomoću sljedećih matrica:

5. Dokažite da .

Izračunajte rang i defekt operatora danih sljedećim matricama:

6. . 7. . 8. .

3. Svojstveni vektori i svojstvene vrijednosti linearnog operatora

Razmotrimo linearni operator A koji djeluje u -dimenzionalnom prostoru X.

Definicija. Broj l se naziva svojstvena vrijednost operatora A if , tako da je . U tom slučaju vektor se naziva svojstvenim vektorom operatora A.

Najvažnije svojstvo svojstvenih vektora linearnog operatora jest da svojstveni vektori koji odgovaraju parovima različitih svojstvenih vrijednosti linearno neovisni.

Ako je matrica linearnog operatora A u bazi prostora X, tada se svojstvene vrijednosti l i svojstveni vektori operatora A određuju na sljedeći način:

1. Svojstvene vrijednosti se nalaze kao korijeni karakteristične jednadžbe (algebarska jednadžba th stupnja):

2. Koordinate svih linearno neovisnih svojstvenih vektora koji odgovaraju svakoj pojedinačnoj svojstvenoj vrijednosti dobivaju se rješavanjem sustava homogenih linearnih jednadžbi:

čija matrica ima rang . Temeljna rješenja ovog sustava su vektori stupci koordinata vlastitih vektora.

Korijeni karakteristične jednadžbe također se nazivaju svojstvenim vrijednostima matrice, a rješenja sustava nazivaju se svojstvenim vektorima matrice.

Primjer. Pronađite svojstvene vektore i svojstvene vrijednosti operatora A, navedene u određenoj bazi matricom

1. Za određivanje svojstvenih vrijednosti sastavljamo i rješavamo karakterističnu jednadžbu:

Odatle proizlazi svojstvena vrijednost, njezina višestrukost.

2. Za određivanje svojstvenih vektora sastavljamo i rješavamo sustav jednadžbi:

Ekvivalentni sustav osnovnih jednadžbi ima oblik

Stoga je svaki svojstveni vektor vektor stupac, gdje je c proizvoljna konstanta.

3.1.Operator jednostavne strukture.

Definicija. Linearni operator A koji djeluje u n-dimenzionalnom prostoru naziva se operatorom jednostavne strukture ako odgovara točno n linearno neovisnih svojstvenih vektora. U ovom slučaju moguće je konstruirati prostornu bazu od svojstvenih vektora operatora u kojoj matrica operatora ima najjednostavniji dijagonalni oblik

gdje su svojstvene vrijednosti operatora. Očito vrijedi i obrnuto: ako u nekoj bazi prostora X matrica operatora ima dijagonalni oblik, tada se baza sastoji od svojstvenih vektora operatora.

Linearni operator A je operator jednostavne strukture ako i samo ako svaka svojstvena vrijednost višestrukosti odgovara točno linearno neovisnim svojstvenim vektorima. Budući da su svojstveni vektori rješenja sustava jednadžbi, svaki korijen karakteristične jednadžbe višestrukosti mora odgovarati matrici ranga.

Svaka matrica veličine koja odgovara jednostavnom strukturnom operatoru slična je dijagonalnoj matrici

gdje prijelazna matrica T iz izvorne baze u bazu svojstvenih vektora ima kao svoje stupce vektore stupce iz koordinata svojstvenih vektora matrice (operator A).

Primjer. Smanjite matricu linearnog operatora na dijagonalni oblik

Napravimo karakterističnu jednadžbu i pronađimo joj korijene.

Odakle dolaze vlastite vrijednosti mnogostrukosti i mnogostrukosti?

Prva svojstvena vrijednost. Odgovara vlastitim vektorima čije su koordinate

sustavno rješenje

Rang ovog sustava je 3, tako da postoji samo jedno neovisno rješenje, na primjer, vektor .

Svojstveni vektori koji odgovaraju određeni su sustavom jednadžbi

čiji je rang 1 i stoga postoje tri linearno neovisna rješenja, npr.

Dakle, svaka svojstvena vrijednost mnogostrukosti odgovara točno linearno neovisnim svojstvenim vektorima i stoga je operator operator jednostavne strukture. Prijelazna matrica T ima oblik

a veza između sličnih matrica određena je relacijom

Zadaci

Pronađite svojstvene vektore i svojstvene vrijednosti

linearni operatori definirani u određenoj bazi matricama:

Odredite koji se od sljedećih linearnih operatora može svesti na dijagonalni oblik prelaskom na novu bazu. Pronađite ovu bazu i njezinu odgovarajuću matricu:

10. Dokažite da su svojstveni vektori linearnog operatora koji odgovaraju različitim svojstvenim vrijednostima linearno neovisni.

11. Dokažite da ako linearni operator A koji djeluje u , ima n različitih vrijednosti, tada svaki linearni operator B komutira s A, ima bazu svojstvenih vektora i svaki svojstveni vektor od A bit će svojstveni vektor od B.

INVARIJANTNI PODPROSTORI

Definicija 1.. Za potprostor L linearnog prostora X kaže se da je invarijantan prema operatoru A koji djeluje u X ako za svaki vektor njegova slika također pripada .

Glavna svojstva invarijantnih potprostora određena su sljedećim relacijama:

1. Ako su i invarijantni podprostori u odnosu na operator A, tada su njihov zbroj i presjek također invarijantni u odnosu na operator A.

2. Ako je prostor X rastavljen na izravni zbroj podprostora i () i invarijantan je u odnosu na A, tada je matrica operatora u bazi, koja je unija baza, blok matrica.

gdje su kvadratne matrice, 0 je nula matrica.

3. U svakom potprostoru invarijantnom u odnosu na operator A, operator ima barem jedan svojstveni vektor.

Primjer 1. Promotrimo jezgru nekog operatora A koji djeluje u X. Po definiciji. Neka . Tada , budući da je nulti vektor sadržan u svakom linearnom potprostoru. Prema tome, kernel je potprostor invarijantan pod A.

Primjer 2. Neka je u nekoj bazi prostora X operator A zadan matricom definiranom jednadžbom i

5. Dokažite da će svaki potprostor koji je invarijantan prema nedegeneriranom operatoru A također biti invarijantan prema inverznom operatoru.

6. Neka linearna transformacija A -dimenzionalnog prostora u svojoj bazi ima dijagonalnu matricu s različitim elementima na dijagonali. Pronađite sve potprostore invarijantne pod A i odredite njihov broj.

Promjena koordinata vektora i matrice operatora pri prelasku na novu bazu

Neka linearni operator djeluje iz prostora u sebe i neka su odabrane dvije baze u linearnom prostoru: i Rastavimo "nove" bazične vektore na linearne kombinacije "starih" bazičnih vektora:

Matrica koja stoji ovdje Kolona čiji je koordinatni stupac vektora te baze u “staroj” bazi naziva se prijelazna matrica sa “stare” baze na “novu”“. Ako su sada koordinate vektora u “staroj” bazi, a koordinate istog vektora u “novoj” bazi, tada vrijedi jednakost

Budući da je proširenje u bazu jedinstveno, slijedi da

Dobiven je sljedeći rezultat.

Teorem 1.Koordinate vektora u bazi i koordinate istog vektora u bazi povezane su relacijama (2), gdje je matrica prijelaza iz “stare” baze u “novu”.

Pogledajmo sada kako su matrice i isti operator međusobno povezani u različitim bazama i prostorima Matrica i definirani su jednakostima Neka je ova jednakost u bazi ekvivalentna matričnoj jednakosti

a u bazi na matričnu jednakost (ovdje se koriste iste oznake kao u (1)). Koristeći teorem (1), imat ćemo

budući da je stupac proizvoljan, dobivamo jednakost

Sljedeći rezultat je dokazan.

Teorem 2.Ako je matrica nekog operatora u bazi i matrica istog operatora u bazi Da

Napomena 1. Dvije proizvoljne matrice i povezane relacijom gdje je neka nesingularna matrica nazivaju se sličnim matricama. Dakle, dvije matrice istog operatora u različitim bazama su slične.

Primjer 1. Operatorska matrica u bazi ima oblik

Nađi matricu ovog operatora u bazi. Izračunaj koordinate vektora u bazi

Riješenje. Matrica prijelaza sa stare baze na novu i njena inverzna matrica imaju oblik

stoga će prema teoremu 2 matrica operatora i nove baze biti sljedeća:

Napomena 2. Ovaj rezultat možemo generalizirati na operatore koji djeluju iz jednog linearnog prostora u drugi. Neka operator djeluje iz linearnog prostora u drugi linearni prostor i neka su u prostoru odabrane dvije baze: i i u prostoru – dvije baze i Tada možemo konstruirati dvije matrice i linearni operator

i dvije matrice i prijelazi sa “starih” baza na “nove”:

Lako je pokazati da u tom slučaju jednakost vrijedi

Neka nam je dan linearni operator koji djeluje iz linearnog prostora u linearni prostor. Sljedeći koncepti korisni su u rješavanju linearnih jednadžbi.

Definicija 1. Operator kernel naziva skup

Slika operatera naziva skup

Nije teško dokazati sljedeću tvrdnju.

Teorem 3.Jezgra i slika linearnog operatora su linearni podprostori prostora i, respektivno, i vrijedi jednakost

Za izračun jezgre operatora potrebno je jednadžbu napisati u matričnom obliku (odabirom baza u razmacima i redom) i riješiti odgovarajući algebarski sustav jednadžbi. Objasnimo sada kako se može izračunati slika operatora.

Neka je matrica operatora u bazama i Označimo s th stupac matrice. Pripadnost vektora slici znači da postoje brojevi takvi da je vektorski stupac predstavljen kao t.j. je element prostora linearnih kombinacija stupaca matrice. Nakon što smo odabrali bazu u tom prostoru (na primjer, najveći skup linearno neovisnih stupaca matrice), prvo izračunamo sliku matrični operator: i zatim izgradite sliku operatora:

Navedimo primjer izračuna jezgre i slike operatora koji djeluje iz prostora u sebe. U ovom slučaju baze se podudaraju.

Primjer 2. Naći matricu, jezgru i sliku operatora projekcije na ravninu (trodimenzionalni prostor geometrijskih vektora).

Riješenje. Odaberimo neku bazu u prostoru (na primjer, standardnu ​​bazu). U ovoj bazi se matrica operatora projekcije nalazi iz jednakosti Nađimo slike baznih vektora. Budući da ravnina prolazi kroz os tada

Tako,

To znači da matrica operatora ima oblik

Jezgra matričnog operatora izračunava se iz jednadžbe

Tako,

(proizvoljna konstanta).

Slika matričnog operatora prevučena je svim linearno neovisnim stupcima matrice, tj.

(proizvoljne konstante).

U vektorski prostor V nad proizvoljnim poljem P postaviti na linearno operator .

Definicija 9.8. Jezgra linearni operator  je skup vektora u prostoru V, čija je slika nulti vektor. Prihvaćeno oznaka za ovaj skup: Ker, tj.

Ker = {x | (x) = o}.

Teorem 9.7. Jezgra linearnog operatora je potprostor prostora V.

Definicija 9.9. Dimenzija naziva se jezgra linearnog operatora mana linearni operator. dim Ker = d.

Definicija 9.10.Na način linearni operator  je skup slika prostorni vektori V. Notacija za ovaj skup im, tj. im = {(x) | x V}.

Teorem 9.8. Slika linearni operator je podprostor prostora V.

Definicija 9.11. Dimenzija slika linearnog operatora naziva se rang linearni operator. dim im = r.

Teorem 9.9. Prostor V je izravni zbroj jezgre i slike linearnog operatora navedenog u njoj. Zbroj ranga i defekta linearnog operatora jednak je dimenziji prostora V.

Primjer 9.3. 1) U svemiru R[x] ( 3) pronaći rang i nedostatak operater diferencijacija. Nađimo one polinome čija je derivacija jednaka nuli. To su dakle polinomi nultog stupnja Ker = {f | f = c) I d= 1. Izvodnice polinoma čiji stupanj nije veći od tri čine skup polinoma čiji stupanj nije veći od dva, dakle, im =R[x] ( 2) i r = 3.

2) Ako je linearna operator je zadan matricom M(), tada se mora riješiti da bi se pronašla njegova jezgra jednadžba ( x) = O, koji u obliku matrice izgleda ovako: M()[x] = [O]. Iz Slijedi da je osnova jezgre linearnog operatora temeljni skup rješenja homogenog sustava linearnih jednadžbi s glavnom matricom M(). Sustav generatora slike linearnog operatora čine vektore ( e 1), (e 2), …, (e n). Osnova ovog sustava vektora daje osnovu slike linearnog operatora.

9.6. Invertibilni linearni operatori

Definicija9.12. Linearno poziva se operator  reverzibilan, ako postoji linearni operater ψ takav što se radi jednakost ψ = ψ = , gdje je  operator identiteta.

Teorem 9.10. Ako je linearna operater  reverzibilan, Da operater ψ definira se jedinstveno i naziva se obrnuti Za operator .

U ovom slučaju operator, inverzan operatoru , označeno  –1.

Teorem 9.11. Linearni operator  je invertibilan ako i samo ako je njegova matrica invertibilna M(), dok M( –1) = (M()) –1 .

Iz ovog teorema slijedi da je rang invertibilnog linearnog operatora jednak dimenzije prostora, a defekt je nula.

Primjer 9.4 1) Odredite je li linearno invertibilno operator , ako je ( x) = (2x 1 – x 2 , –4x 1 + 2x 2).

Riješenje. Kreirajmo matricu za ovaj linearni operator: M() = . Jer
= 0 zatim matrica M() je ireverzibilan, što znači da je ireverzibilan i linearan operater .

2) Pronaći linearni operater, leđa operator , if (x) = (2x 1 + x 2 , 3x 1 + 2x 2).

Riješenje. Matrica ovog linearnog operator jednako M() =
, je reverzibilan, jer | M()| ≠ 0. (M()) –1 =
, dakle  –1 = (2x 1 – x 2 , –3x 1 + 2x 2).