किसी फ़ंक्शन उदाहरण के शून्य कैसे खोजें। फ़ंक्शन शून्य क्या हैं और उन्हें कैसे निर्धारित करें। सीमित एवं असीमित कार्य। निरंतर और

तर्क मान जेड जिस पर एफ(जेड) शून्य पर जाता है कहा जाता है। शून्य बिंदु, अर्थात। अगर एफ(ए) = 0, तो ए - शून्य बिंदु.

हार।डॉट एबुलाया शून्य आदेशएन , अगर एफकेपी को फॉर्म में दर्शाया जा सकता है एफ(जेड) = , कहाँ
विश्लेषणात्मक कार्य और
0.

इस मामले में, टेलर श्रृंखला में फ़ंक्शन का विस्तार (43), पहला एन गुणांक शून्य हैं

= =

वगैरह। के लिए शून्य का क्रम निर्धारित करें
और (1-कोस जेड) पर जेड = 0

=
=

शून्य प्रथम क्रम

1 - क्योंकि जेड =
=

शून्य दूसरा क्रम

हार।डॉट जेड =
बुलाया अनंत पर बिंदुऔर शून्यकार्य एफ(जेड), अगर एफ(
) = 0. ऐसे फ़ंक्शन को नकारात्मक शक्तियों में एक श्रृंखला में विस्तारित किया जा सकता है जेड : एफ(जेड) =
. अगर पहला एन गुणांक शून्य के बराबर हैं, तो हम पहुंचते हैं शून्य आदेश एन अनंत पर एक बिंदु पर: एफ(जेड) = जेड - एन
.

पृथक एकवचन बिंदुओं को इसमें विभाजित किया गया है: ए) हटाने योग्य एकवचन बिंदु; बी) व्यवस्था के ध्रुवएन; वी) मूलतः एकवचन बिंदु.

डॉट एबुलाया हटाने योग्य एकवचन बिंदुकार्य एफ(जेड) मैं मोटा जेड
ए लिम एफ(जेड) = साथ -अंतिम संख्या .

डॉट एबुलाया आदेश का ध्रुवएन (एन 1) कार्य एफ(जेड), यदि उलटा कार्य
= 1/ एफ(जेड) का ऑर्डर शून्य है एनबिंदु पर एक।ऐसे फ़ंक्शन को हमेशा इस रूप में दर्शाया जा सकता है एफ(जेड) =
, कहाँ
- विश्लेषणात्मक कार्य और
.

डॉट एबुलाया मूलतः एक विशेष बिंदुकार्य एफ(जेड), मैं मोटा जेड
ए लिम एफ(जेड) मौजूद नहीं होना।

लॉरेंट श्रृंखला

आइए हम वलय अभिसरण क्षेत्र के मामले पर विचार करें आर < | जेड 0 – ए| < आरएक बिंदु पर केन्द्रित एसमारोह के लिए एफ(जेड). आइए दो नए मंडलों का परिचय दें एल 1 (आर) और एल 2 (आर) एक बिंदु के साथ रिंग की सीमाओं के पास जेडउनके बीच 0. आइए रिंग का एक कट बनाएं, कट के किनारों के साथ वृत्तों को जोड़ें, एक साधारण रूप से जुड़े हुए क्षेत्र की ओर बढ़ें और अंदर जाएं

कॉची इंटीग्रल फॉर्मूला (39) से हमें वेरिएबल z पर दो इंटीग्रल मिलते हैं

एफ(जेड 0) =
+
, (42)

जहां एकीकरण विपरीत दिशाओं में जाता है।

अभिन्न ओवर के लिए एल 1 शर्त पूरी होती है | जेड 0 – ए | > | जेड – ए |, और अभिन्न ओवर के लिए एल 2 विपरीत स्थिति | जेड 0 – ए | < | जेड – ए |. इसलिए, कारक 1/( जेड – जेड 0) अभिन्न ओवर में श्रृंखला (ए) में विस्तार करें एल 2 और श्रृंखला में (बी) अभिन्न ओवर में एल 1 . परिणामस्वरूप, हमें विस्तार प्राप्त होता है एफ(जेड) रिंग एरिया में लॉरेंट श्रृंखलासकारात्मक एवं नकारात्मक शक्तियों द्वारा ( जेड 0 – ए)

एफ(जेड 0) =
ए एन (जेड 0 -ए) एन (43)

कहाँ ए एन =
=
;ए -एन =

सकारात्मक शक्तियों में विस्तार (जेड 0 - ए) बुलाया सही भागलॉरेंट शृंखला (टेलर शृंखला) और नकारात्मक शक्तियों में विस्तार को कहा जाता है। मुख्य हिस्सालॉरेंट श्रृंखला.

अगर घेरे के अंदर एल 1 कोई एकवचन बिंदु नहीं हैं और फ़ंक्शन विश्लेषणात्मक है, तो (44) में पहला इंटीग्रल कॉची के प्रमेय द्वारा शून्य के बराबर है और फ़ंक्शन के विस्तार में केवल सही भाग रहता है। विस्तार में नकारात्मक शक्तियाँ (45) केवल तभी प्रकट होती हैं जब आंतरिक घेरे के भीतर विश्लेषणात्मकता का उल्लंघन होता है और अलग-अलग एकवचन बिंदुओं के पास फ़ंक्शन का वर्णन करने के लिए काम करते हैं।

लॉरेंट श्रृंखला (45) का निर्माण करना एफ(जेड) आप एक सामान्य सूत्र का उपयोग करके विस्तार गुणांक की गणना कर सकते हैं या इसमें शामिल प्राथमिक कार्यों के विस्तार का उपयोग कर सकते हैं एफ(जेड).

पदों की संख्या ( एन) लॉरेंट श्रृंखला का मुख्य भाग एकवचन बिंदु के प्रकार पर निर्भर करता है: हटाने योग्य एकवचन बिंदु (एन = 0) ; मूलतः एकवचन बिंदु (एन
); खंभाएन-वाह आदेश!(एन - अंतिम संख्या)।

और के लिए एफ(जेड) = डॉट जेड = 0 हटाने योग्य एकवचन बिंदु,क्योंकि कोई मुख्य भाग नहीं है. एफ(जेड) = (जेड -
) = 1 -

बी) के लिए एफ(जेड) = डॉट जेड = 0 - प्रथम क्रम का खंभा

एफ(जेड) = (जेड -
) = -

ग) के लिए एफ(जेड) = इ 1 / जेडडॉट जेड = 0 - मूलतः एकवचन बिंदु

एफ(जेड) = इ 1 / जेड =

अगर एफ(जेड) डोमेन में विश्लेषणात्मक है डीके अपवाद के साथ एमपृथक एकवचन बिंदु और | जेड 1 | < |जेड 2 | < . . . < |जेड एम| , फिर शक्तियों में फ़ंक्शन का विस्तार करते समय जेडपूरे विमान को विभाजित किया गया है एम+ 1 अंगूठी | जेड मैं | < | जेड | < | जेड मैं+1 | और लॉरेंट श्रृंखला में प्रत्येक रिंग का स्वरूप अलग-अलग होता है। शक्तियों में विस्तार होने पर ( जेड – जेड मैं ) लॉरेंट श्रृंखला का अभिसरण क्षेत्र वृत्त है | जेड – जेड मैं | < आर, कहाँ आर - निकटतम एकवचन बिंदु से दूरी।

वगैरह। आइए फ़ंक्शन का विस्तार करें एफ(जेड) =शक्तियों में लॉरेंट श्रृंखला में जेडऔर ( जेड - 1).

समाधान। आइए फ़ंक्शन को फॉर्म में प्रस्तुत करें एफ(जेड) = - जेड 2 . हम ज्यामितीय प्रगति के योग के लिए सूत्र का उपयोग करते हैं
. घेरे में |z|< 1 ряд сходится и एफ(जेड) = - जेड 2 (1 + जेड + जेड 2 + जेड 3 + जेड 4 + . . .) = - जेड 2 - जेड 3 - जेड 4 - . . . , अर्थात। अपघटन में केवल शामिल है सहीभाग। आइए वृत्त |z| के बाहरी क्षेत्र की ओर चलें > 1. आइए फ़ंक्शन को फॉर्म में प्रस्तुत करें
, जहां 1/| जेड| < 1, и получим разложение एफ(जेड) = जेड
=जेड + 1 +

क्योंकि , शक्तियों में किसी फ़ंक्शन का विस्तार ( जेड - 1) दिखता है एफ(जेड) = (जेड - 1) -1 + 2 + (जेड - 1) सबके लिए
1.

वगैरह। फ़ंक्शन को लॉरेंट श्रृंखला में विस्तारित करें एफ(जेड) =
: ए) डिग्री द्वारा जेडएक घेरे में | जेड| < 1; b) по степеням जेड अंगूठी 1< |जेड| < 3 ; c) по степеням (जेड – 2).समाधान. आइए फ़ंक्शन को सरल भिन्नों में विघटित करें
= =+=
. शर्तों से जेड =1
ए = -1/2 , जेड =3
बी = ½.

ए) एफ(जेड) = ½ [
] = ½ [
-(1/3)
], के साथ | जेड|< 1.

बी) एफ(जेड) = - ½ [
+
] = - (
), 1 पर< |जेड| < 3.

साथ) एफ(जेड) = ½ [
]= - ½ [
] =

= - ½ = -
, साथ |2 - जेड| < 1

यह त्रिज्या 1 पर केन्द्रित एक वृत्त है जेड = 2 .

कुछ मामलों में, शक्ति श्रृंखला को ज्यामितीय प्रगति के एक सेट तक कम किया जा सकता है, और इसके बाद उनके अभिसरण के क्षेत्र को निर्धारित करना आसान होता है।

वगैरह। श्रृंखला के अभिसरण की जांच करें

. . . + + + + 1 + () + () 2 + () 3 + . . .

समाधान। यह दो ज्यामितीय प्रगतियों का योग है क्यू 1 = , क्यू 2 = () . यह उनके अभिसरण की स्थितियों से निम्नानुसार है < 1 , < 1 или |जेड| > 1 , |जेड| < 2 , т.е. область сходимости ряда кольцо 1 < |जेड| < 2 .

समारोहसबसे महत्वपूर्ण गणितीय अवधारणाओं में से एक है। कार्य - परिवर्तनशील निर्भरता परपरिवर्तनशील से एक्स, यदि प्रत्येक मान एक्सएकल मान से मेल खाता है पर. चर एक्सस्वतंत्र चर या तर्क कहा जाता है। चर परआश्रित चर कहलाता है। स्वतंत्र चर (चर) के सभी मान एक्स) फ़ंक्शन की परिभाषा का क्षेत्र बनाएं। वे सभी मान जो आश्रित चर लेता है (चर)। य), फ़ंक्शन के मानों की श्रेणी बनाएं।

फ़ंक्शन ग्राफ़निर्देशांक तल के सभी बिंदुओं के समुच्चय को कॉल करें, जिसके भुज तर्क के मानों के बराबर हैं, और निर्देशांक फ़ंक्शन के संबंधित मानों के बराबर हैं, अर्थात के मान चर को भुज अक्ष के अनुदिश आलेखित किया जाता है एक्स, और चर के मान को ऑर्डिनेट अक्ष के साथ प्लॉट किए जाते हैं य. किसी फ़ंक्शन को ग्राफ़ करने के लिए, आपको फ़ंक्शन के गुणों को जानना होगा। फ़ंक्शन के मुख्य गुणों पर नीचे चर्चा की जाएगी!

किसी फ़ंक्शन का ग्राफ़ बनाने के लिए, हम अपने प्रोग्राम - ग्राफ़िंग फ़ंक्शंस ऑनलाइन का उपयोग करने की अनुशंसा करते हैं। यदि इस पृष्ठ पर सामग्री का अध्ययन करते समय आपके कोई प्रश्न हैं, तो आप उन्हें हमेशा हमारे मंच पर पूछ सकते हैं। इसके अलावा मंच पर वे आपको गणित, रसायन विज्ञान, ज्यामिति, संभाव्यता सिद्धांत और कई अन्य विषयों में समस्याओं को हल करने में मदद करेंगे!

कार्यों के मूल गुण।

1) फ़ंक्शन डोमेन और फ़ंक्शन रेंज.

किसी फ़ंक्शन का डोमेन सभी वैध मान्य तर्क मानों का सेट है एक्स(चर एक्स), जिसके लिए फ़ंक्शन वाई = एफ(एक्स)दृढ़ निश्चय वाला।
किसी फ़ंक्शन की सीमा सभी वास्तविक मानों का समुच्चय है य, जिसे फ़ंक्शन स्वीकार करता है।

प्रारंभिक गणित में, कार्यों का अध्ययन केवल वास्तविक संख्याओं के सेट पर किया जाता है।

2) फ़ंक्शन शून्य.

फ़ंक्शन शून्य उस तर्क का मान है जिस पर फ़ंक्शन का मान शून्य के बराबर होता है।

3) किसी फ़ंक्शन के स्थिर चिह्न का अंतराल.

किसी फ़ंक्शन के स्थिर चिह्न के अंतराल तर्क मानों के सेट होते हैं जिन पर फ़ंक्शन मान केवल सकारात्मक या केवल नकारात्मक होते हैं।

4) फ़ंक्शन की एकरसता.

एक बढ़ता हुआ फ़ंक्शन (एक निश्चित अंतराल में) एक ऐसा फ़ंक्शन होता है जिसमें इस अंतराल से तर्क का बड़ा मान फ़ंक्शन के बड़े मान से मेल खाता है।

एक घटता हुआ फ़ंक्शन (एक निश्चित अंतराल में) एक ऐसा फ़ंक्शन होता है जिसमें इस अंतराल से तर्क का बड़ा मान फ़ंक्शन के छोटे मान से मेल खाता है।

5) सम (विषम) फ़ंक्शन.

एक सम फलन एक ऐसा फलन है जिसकी परिभाषा का क्षेत्र मूल और किसी के संबंध में सममित है एक्सपरिभाषा के क्षेत्र से समानता एफ(-एक्स) = एफ(एक्स). एक सम फलन का ग्राफ कोटि के प्रति सममित होता है।

एक विषम फलन एक ऐसा फलन है जिसकी परिभाषा का क्षेत्र मूल और किसी के संबंध में सममित है एक्सपरिभाषा के क्षेत्र से समानता सत्य है एफ(-एक्स) = - एफ(एक्स). एक विषम फलन का ग्राफ मूल बिन्दु के प्रति सममित होता है।

6) सीमित एवं असीमित कार्य.

यदि कोई धनात्मक संख्या M ऐसी हो कि |f(x)| तो किसी फ़ंक्शन को परिबद्ध कहा जाता है ≤ x के सभी मानों के लिए M. यदि ऐसी कोई संख्या मौजूद नहीं है, तो फ़ंक्शन असीमित है।

7) समारोह की आवधिकता.

एक फलन f(x) आवर्त है यदि कोई शून्येतर संख्या T है जैसे कि किसी x f(x+T) = f(x) के लिए। इस सबसे छोटी संख्या को फलन का आवर्त कहा जाता है। सभी त्रिकोणमितीय फलन आवर्ती होते हैं। (त्रिकोणमितीय सूत्र).

किसी फ़ंक्शन के इन गुणों का अध्ययन करने के बाद, आप आसानी से फ़ंक्शन का पता लगा सकते हैं और फ़ंक्शन के गुणों का उपयोग करके, आप फ़ंक्शन का एक ग्राफ़ बना सकते हैं। सत्य सारणी, गुणन सारणी, आवर्त सारणी, अवकलज सारणी और समाकलन सारणी के बारे में भी सामग्री देखें।

फ़ंक्शन शून्य

फ़ंक्शन शून्य क्या हैं? किसी फ़ंक्शन के शून्य को विश्लेषणात्मक और ग्राफ़िक रूप से कैसे निर्धारित करें?

फ़ंक्शन शून्य- ये तर्क मान हैं जिन पर फ़ंक्शन शून्य के बराबर है।

सूत्र y=f(x) द्वारा दिए गए फ़ंक्शन के शून्य को खोजने के लिए, आपको समीकरण f(x)=0 को हल करने की आवश्यकता है।

यदि समीकरण का कोई मूल नहीं है, तो फ़ंक्शन का कोई शून्य नहीं है।

1) रैखिक फलन y=3x+15 के शून्यक ज्ञात कीजिए।

फ़ंक्शन के शून्य ज्ञात करने के लिए, समीकरण 3x+15 =0 को हल करें।

इस प्रकार, फ़ंक्शन का शून्य y=3x+15 - x= -5 है।

2) द्विघात फलन f(x)=x²-7x+12 के शून्यक ज्ञात कीजिए।

फ़ंक्शन के शून्य ज्ञात करने के लिए, द्विघात समीकरण को हल करें

इसके मूल x1=3 और x2=4 इस फ़ंक्शन के शून्य हैं।

3) फ़ंक्शन के शून्य ज्ञात करें

यदि हर गैर-शून्य है तो भिन्न का कोई अर्थ नहीं है। इसलिए, x²-1≠0, x² ≠ 1, x ≠±1. अर्थात्, किसी दिए गए फ़ंक्शन की परिभाषा का क्षेत्र (डीओ)

समीकरण x²+5x+4=0 x1=-1 x2=-4 की जड़ों में से, केवल x=-4 परिभाषा के क्षेत्र में शामिल है।

ग्राफ़िक रूप से दिए गए किसी फ़ंक्शन के शून्य को खोजने के लिए, आपको एब्सिस्सा अक्ष के साथ फ़ंक्शन ग्राफ़ के प्रतिच्छेदन बिंदु खोजने की आवश्यकता है।

यदि ग्राफ़ ऑक्स-अक्ष को प्रतिच्छेद नहीं करता है, तो फ़ंक्शन में कोई शून्य नहीं है।

जिस फ़ंक्शन का ग्राफ चित्र में दिखाया गया है उसमें चार शून्य हैं -

बीजगणित में, किसी फ़ंक्शन के शून्य खोजने की समस्या एक स्वतंत्र कार्य के रूप में और अन्य समस्याओं को हल करते समय उत्पन्न होती है, उदाहरण के लिए, किसी फ़ंक्शन का अध्ययन करते समय, असमानताओं को हल करते समय, आदि।

www.algebraclass.ru

फ़ंक्शन शून्य नियम

कार्यों की बुनियादी अवधारणाएँ और गुण

नियम (का कानून) पत्राचार। मोनोटोनिक फ़ंक्शन .

सीमित एवं असीमित कार्य। निरंतर और

असंतत कार्य . सम और विषम कार्य।

आवधिक कार्य. समारोह की अवधि.

फ़ंक्शन शून्य . अनंतस्पर्शी .

परिभाषा का क्षेत्र और किसी फ़ंक्शन के मानों की सीमा। प्रारंभिक गणित में, कार्यों का अध्ययन केवल वास्तविक संख्याओं के सेट पर किया जाता है आर . इसका मतलब यह है कि फ़ंक्शन तर्क केवल उन्हीं वास्तविक मानों को ले सकता है जिनके लिए फ़ंक्शन परिभाषित है, अर्थात। यह भी केवल वास्तविक मूल्यों को ही स्वीकार करता है। गुच्छा एक्स सभी वैध वैध तर्क मान एक्स, जिसके लिए फ़ंक्शन य = एफ (एक्स) परिभाषित है, कहा जाता है फ़ंक्शन का डोमेन. गुच्छा वाई सभी वास्तविक मूल्य य, जिसे फ़ंक्शन स्वीकार करता है, कहलाता है फ़ंक्शन रेंज. अब हम फ़ंक्शन की अधिक सटीक परिभाषा दे सकते हैं: नियम (कानून) सेटों के बीच पत्राचार का एक्सऔर वाई , जिसके अनुसार सेट से प्रत्येक तत्व के लिए एक्सआप सेट से एक और केवल एक तत्व पा सकते हैं वाई, को एक फ़ंक्शन कहा जाता है .

इस परिभाषा से यह निष्कर्ष निकलता है कि किसी फ़ंक्शन को परिभाषित माना जाता है यदि:

- फ़ंक्शन की परिभाषा का क्षेत्र निर्दिष्ट है एक्स ;

- फ़ंक्शन रेंज निर्दिष्ट है वाई ;

- पत्राचार का नियम (कानून) ज्ञात है, और ऐसा प्रत्येक के लिए

तर्क मान, केवल एक फ़ंक्शन मान पाया जा सकता है।

फ़ंक्शन की विशिष्टता की यह आवश्यकता अनिवार्य है।

मोनोटोनिक फ़ंक्शन। यदि तर्क के किन्हीं दो मानों के लिए एक्स 1 और एक्सशर्त के 2 एक्स 2 > एक्स 1 अनुसरण करता है एफ (एक्स 2) > एफ (एक्स 1), फिर फ़ंक्शन एफ (एक्स) कहा जाता है की बढ़ती; यदि किसी के लिए एक्स 1 और एक्सशर्त के 2 एक्स 2 > एक्स 1 अनुसरण करता है एफ (एक्स 2)

चित्र 3 में दिखाया गया कार्य सीमित है, लेकिन एकरस नहीं है। चित्र 4 में फ़ंक्शन बिल्कुल विपरीत, मोनोटोनिक, लेकिन असीमित है। (कृपया इसे समझाएं!)

निरंतर और असंतत कार्य. समारोह य = एफ (एक्स) कहा जाता है निरंतर बिंदु पर एक्स = ए, अगर:

1) फ़ंक्शन को तब परिभाषित किया जाता है एक्स = ए, अर्थात। एफ (ए) मौजूद;

2) मौजूद है परिमितसीमा लिम एफ (एक्स) ;

यदि इनमें से कम से कम एक शर्त पूरी नहीं होती है, तो फ़ंक्शन को कॉल किया जाता है विस्फोटकबिंदु पर एक्स = ए .

यदि फ़ंक्शन निरंतर है सब लोग इसकी परिभाषा के क्षेत्र के बिंदु, तो इसे कहा जाता है सतत कार्य.

सम और विषम कार्य. यदि के लिए कोई एक्सफ़ंक्शन की परिभाषा के क्षेत्र से निम्नलिखित मान्य है: एफ (— एक्स) = एफ (एक्स), फिर फ़ंक्शन को कॉल किया जाता है यहां तक ​​की; यदि ऐसा होता है: एफ (— एक्स) = — एफ (एक्स), फिर फ़ंक्शन को कॉल किया जाता है विषम. एक सम फ़ंक्शन का ग्राफ़ Y अक्ष के बारे में सममित(चित्र 5), एक विषम फलन का ग्राफ़ सिम उत्पत्ति के संबंध में मीट्रिक(चित्र 6)।

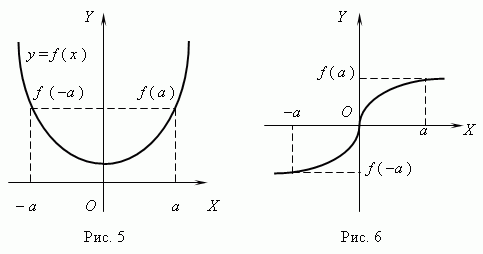
आवधिक कार्य. समारोह एफ (एक्स) — आवधिक, यदि ऐसी कोई बात मौजूद है शून्येतरसंख्या टीकिस लिए कोई एक्सफ़ंक्शन की परिभाषा के क्षेत्र से निम्नलिखित मान्य है: एफ (एक्स + टी) = एफ (एक्स). यह कम से कमनंबर पर कॉल किया जाता है समारोह की अवधि. सभी त्रिकोणमितीय फलन आवर्ती होते हैं।

उदाहरण 1। उस पाप को सिद्ध करो एक्स 2 की अवधि है.

समाधान: हम जानते हैं कि पाप ( एक्स+ 2 एन) = पाप एक्स, कहाँ एन= 0, ± 1, ± 2, ...

इसलिए जोड़ 2 एनसाइन तर्क के लिए

इसका मान बदलता है ई. क्या इसके साथ कोई और नंबर भी है

चलिए ऐसा दिखावा करते हैं पी- ऐसी संख्या, यानी समानता:

किसी भी मूल्य के लिए मान्य एक्स. लेकिन फिर यह है

जगह और पर एक्स= /2, अर्थात

पाप(/2 + पी) = पाप / 2 = 1.

लेकिन न्यूनीकरण सूत्र के अनुसार पाप (/2 + पी) = क्योंकि पी. तब

पिछली दो समानताओं से यह इस प्रकार है कि cos पी= 1, लेकिन हम

हम जानते हैं कि यह तभी सत्य है जब पी = 2 एन. सबसे छोटे से

2 से गैर-शून्य संख्या एन 2 है तो यह संख्या

और एक अवधि पाप है एक्स. इसे इसी प्रकार सिद्ध किया जा सकता है कि 2

कॉस के लिए भी एक अवधि है एक्स .

साबित करें कि कार्य tan हैं एक्सऔर खाट एक्सअवधि है.

उदाहरण 2. फ़ंक्शन पाप 2 की अवधि कौन सी संख्या है एक्स ?

समाधान: पाप 2 पर विचार करें एक्स= पाप(2 एक्स+ 2 एन) = पाप [2( एक्स + एन) ] .

हम इसे जोड़ते हुए देखते हैं एनतर्क के लिए एक्स, बदलना मत

फ़ंक्शन मान. सबसे छोटी गैर-शून्य संख्या

से एनहै, अतः यह अवधि पाप 2 है एक्स .

फ़ंक्शन शून्य. वह तर्क मान जिस पर फ़ंक्शन 0 के बराबर है, कहलाता है शून्य ( रूट) फ़ंक्शन. किसी फ़ंक्शन में एकाधिक शून्य हो सकते हैं. उदाहरण के लिए, फ़ंक्शन य = एक्स (एक्स + 1) (एक्स- 3) में तीन शून्य होते हैं: एक्स = 0, एक्स = — 1, एक्स= 3. ज्यामितीय रूप से शून्य फ़ंक्शन – यह अक्ष के साथ फ़ंक्शन ग्राफ़ के प्रतिच्छेदन बिंदु का भुज है एक्स .

चित्र 7 शून्य वाले फ़ंक्शन का ग्राफ़ दिखाता है: एक्स = ए , एक्स = बीऔर एक्स = सी .

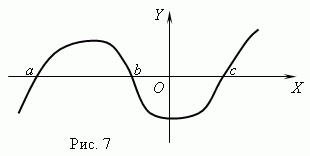
स्पर्शोन्मुख. यदि किसी फ़ंक्शन का ग्राफ मूल बिंदु से दूर जाते हुए अनिश्चित काल तक एक निश्चित रेखा के पास पहुंचता है, तो इस रेखा को कहा जाता है अनंतस्पर्शी.

विषय 6. "अंतराल विधि।"

यदि x x 0 के लिए f (x) f (x 0), तो फ़ंक्शन f (x) कहा जाता है बिंदु x 0 पर निरंतर.

यदि कोई फ़ंक्शन किसी अंतराल I के प्रत्येक बिंदु पर निरंतर है, तो इसे कहा जाता है अंतराल पर निरंतर I (अंतराल I को कहा जाता है फ़ंक्शन की निरंतरता अंतराल). इस अंतराल पर किसी फ़ंक्शन का ग्राफ़ एक सतत रेखा है, जिसके बारे में वे कहते हैं कि इसे "कागज़ से पेंसिल उठाए बिना खींचा जा सकता है।"

सतत कार्यों की संपत्ति.

यदि अंतराल (ए; बी) पर फ़ंक्शन एफ निरंतर है और गायब नहीं होता है, तो यह इस अंतराल पर एक स्थिर चिह्न बनाए रखता है।

एक चर के साथ असमानताओं को हल करने की एक विधि, अंतराल विधि, इस संपत्ति पर आधारित है। मान लीजिए कि फ़ंक्शन f(x) अंतराल I पर निरंतर है और इस अंतराल में सीमित संख्या में बिंदुओं पर गायब हो जाता है। सतत फलनों के गुण के अनुसार, ये बिंदु I को अंतरालों में विभाजित करते हैं, जिनमें से प्रत्येक में सतत फलन f(x) c एक स्थिर चिह्न बनाए रखता है। इस चिन्ह को निर्धारित करने के लिए, ऐसे प्रत्येक अंतराल से किसी एक बिंदु पर फ़ंक्शन f(x) के मान की गणना करना पर्याप्त है। इसके आधार पर, हम अंतराल विधि का उपयोग करके असमानताओं को हल करने के लिए निम्नलिखित एल्गोरिदम प्राप्त करते हैं।

प्रपत्र की असमानताओं के लिए अंतराल विधि

अंतराल विधि. औसत स्तर।

क्या आप अपनी ताकत का परीक्षण करना चाहते हैं और परिणाम जानना चाहते हैं कि आप एकीकृत राज्य परीक्षा या एकीकृत राज्य परीक्षा के लिए कितने तैयार हैं?

रैखिक प्रकार्य

प्रपत्र के एक फलन को रैखिक कहा जाता है। आइए एक फ़ंक्शन को उदाहरण के रूप में लें। यह 3″> पर सकारात्मक और नकारात्मक है। बिंदु फ़ंक्शन () का शून्य है। आइए संख्या अक्ष पर इस फ़ंक्शन के चिह्न दिखाएं:

हम कहते हैं कि "बिंदु से गुजरने पर फ़ंक्शन संकेत बदल देता है"।

यह देखा जा सकता है कि फ़ंक्शन के चिह्न फ़ंक्शन ग्राफ़ की स्थिति के अनुरूप हैं: यदि ग्राफ़ अक्ष के ऊपर है, तो चिह्न " " है, यदि नीचे यह " " है।

यदि हम परिणामी नियम को एक मनमाना रैखिक फ़ंक्शन के लिए सामान्यीकृत करते हैं, तो हमें निम्नलिखित एल्गोरिदम प्राप्त होता है:

द्विघात फंक्शन

मुझे आशा है कि आपको याद होगा कि द्विघात असमानताओं को कैसे हल करें? यदि नहीं, तो "द्विघात असमानताएँ" विषय पढ़ें। मैं आपको द्विघात फलन के सामान्य रूप की याद दिलाना चाहता हूँ:।

अब आइए याद करें कि द्विघात फलन कौन से चिह्न लेता है। इसका ग्राफ एक परवलय है, और फ़ंक्शन उन लोगों के लिए " " चिह्न लेता है जिनमें परवलय अक्ष के ऊपर है, और " " - यदि परवलय अक्ष के नीचे है:

यदि किसी फ़ंक्शन में शून्य (मान) हैं, तो परवलय अक्ष को दो बिंदुओं पर काटता है - संबंधित द्विघात समीकरण की जड़ें। इस प्रकार, अक्ष को तीन अंतरालों में विभाजित किया जाता है, और प्रत्येक जड़ से गुजरने पर फ़ंक्शन के संकेत बारी-बारी से बदलते हैं।

क्या हर बार परवलय बनाए बिना किसी तरह चिन्ह निर्धारित करना संभव है?

याद रखें कि एक वर्ग त्रिपद को गुणनखंडित किया जा सकता है:

आइए अक्ष पर जड़ों को चिह्नित करें:

हमें याद है कि किसी फ़ंक्शन का चिह्न केवल रूट से गुजरने पर ही बदल सकता है। आइए इस तथ्य का उपयोग करें: तीन अंतरालों में से प्रत्येक के लिए जिसमें अक्ष को जड़ों द्वारा विभाजित किया गया है, यह केवल एक मनमाने ढंग से चुने गए बिंदु पर फ़ंक्शन के संकेत को निर्धारित करने के लिए पर्याप्त है: अंतराल के शेष बिंदुओं पर संकेत समान होगा .

हमारे उदाहरण में: 3″> पर कोष्ठक में दोनों भाव सकारात्मक हैं (उदाहरण के लिए विकल्प: 0″>)। हम अक्ष पर " " चिन्ह लगाते हैं:

खैर, जब (उदाहरण के लिए, विकल्प), दोनों कोष्ठक नकारात्मक हैं, जिसका अर्थ है कि उत्पाद सकारात्मक है:

यह वही है अंतराल विधि: प्रत्येक अंतराल पर कारकों के संकेतों को जानकर, हम संपूर्ण उत्पाद का संकेत निर्धारित करते हैं।

आइए उन मामलों पर भी विचार करें जब फ़ंक्शन में कोई शून्य नहीं है, या केवल एक है।

यदि वे वहां नहीं हैं, तो जड़ें भी नहीं हैं। इसका मतलब यह है कि कोई "जड़ से गुजरना" नहीं होगा। इसका मतलब यह है कि फ़ंक्शन पूरी संख्या रेखा पर केवल एक चिह्न लेता है। इसे किसी फ़ंक्शन में प्रतिस्थापित करके आसानी से निर्धारित किया जा सकता है।

यदि केवल एक जड़ है, तो परवलय अक्ष को छूता है, इसलिए जड़ से गुजरने पर फ़ंक्शन का चिह्न नहीं बदलता है। ऐसी स्थितियों के लिए हम क्या नियम बना सकते हैं?

यदि आप ऐसे फ़ंक्शन का कारक बनाते हैं, तो आपको दो समान कारक मिलते हैं:

और कोई भी वर्गाकार अभिव्यक्ति गैर-नकारात्मक है! इसलिए, फ़ंक्शन का चिह्न नहीं बदलता है. ऐसे मामलों में, हम उस मूल को उजागर करेंगे, जिसके माध्यम से गुजरने पर चिह्न नहीं बदलता है, इसे एक वर्ग के साथ घेरकर:

हम ऐसी जड़ कहेंगे गुणकों.

असमानताओं में अंतराल विधि

अब किसी भी द्विघात असमानता को परवलय बनाए बिना हल किया जा सकता है। द्विघात फलन के चिह्नों को अक्ष पर रखना और असमानता के चिह्न के आधार पर अंतरालों का चयन करना ही पर्याप्त है। उदाहरण के लिए:

आइए अक्ष पर जड़ों को मापें और चिह्न लगाएं:

हमें " " चिन्ह वाले अक्ष के भाग की आवश्यकता है; चूंकि असमानता सख्त नहीं है, इसलिए जड़ें भी समाधान में शामिल हैं:

अब एक तर्कसंगत असमानता पर विचार करें - एक असमानता, जिसके दोनों पक्ष तर्कसंगत अभिव्यक्ति हैं (देखें "तर्कसंगत समीकरण")।

उदाहरण:

एक को छोड़कर सभी कारक यहां "रैखिक" हैं, यानी, उनमें केवल पहली शक्ति के लिए एक चर होता है। अंतराल विधि को लागू करने के लिए हमें ऐसे रैखिक कारकों की आवश्यकता होती है - उनकी जड़ों से गुजरने पर संकेत बदल जाता है। लेकिन गुणक की कोई जड़ नहीं होती। इसका मतलब यह है कि यह हमेशा सकारात्मक होता है (इसे स्वयं जांचें), और इसलिए संपूर्ण असमानता के संकेत को प्रभावित नहीं करता है। इसका मतलब यह है कि हम इसके द्वारा असमानता के बाएँ और दाएँ पक्षों को विभाजित कर सकते हैं, और इस प्रकार इससे छुटकारा पा सकते हैं:

अब सब कुछ वैसा ही है जैसा कि द्विघात असमानताओं के साथ था: हम यह निर्धारित करते हैं कि किन बिंदुओं पर प्रत्येक कारक शून्य हो जाता है, इन बिंदुओं को अक्ष पर चिह्नित करें और संकेतों को व्यवस्थित करें। मैं आपका ध्यान एक बहुत ही महत्वपूर्ण तथ्य की ओर आकर्षित करना चाहता हूं:

सम संख्या के मामले में, हम पहले की तरह ही करते हैं: हम बिंदु के चारों ओर एक वर्ग बनाते हैं और मूल से गुजरते समय चिह्न नहीं बदलते हैं। लेकिन विषम संख्या के मामले में, यह नियम लागू नहीं होता है: मूल से गुजरने पर भी चिह्न बदल जाएगा। इसलिए, हम ऐसे रूट के साथ कुछ भी अतिरिक्त नहीं करते हैं, जैसे कि वह एकाधिक न हो। उपरोक्त नियम सभी सम और विषम शक्तियों पर लागू होते हैं।

हमें उत्तर में क्या लिखना चाहिए?

यदि संकेतों के विकल्प का उल्लंघन किया जाता है, तो आपको बहुत सावधान रहने की आवश्यकता है, क्योंकि यदि असमानता सख्त नहीं है, तो उत्तर में शामिल होना चाहिए सभी छायांकित बिंदु. लेकिन उनमें से कुछ अक्सर अलग-अलग खड़े होते हैं, यानी वे छायांकित क्षेत्र में शामिल नहीं होते हैं। इस मामले में, हम उन्हें उत्तर में पृथक बिंदुओं के रूप में जोड़ते हैं (घुंघराले ब्रेसिज़ में):

उदाहरण (स्वयं निर्णय लें):

उत्तर:

1. यदि कारकों में से यह सरल है, तो यह एक जड़ है, क्योंकि इसे इस रूप में दर्शाया जा सकता है।
   .

किसी फ़ंक्शन का गणितीय प्रतिनिधित्व स्पष्ट रूप से दिखाता है कि कैसे एक मात्रा दूसरी मात्रा के मूल्य को पूरी तरह से निर्धारित करती है। परंपरागत रूप से, संख्यात्मक कार्यों को माना जाता है जो एक संख्या को दूसरे को निर्दिष्ट करते हैं। किसी फ़ंक्शन का शून्य आमतौर पर उस तर्क का मान होता है जिस पर फ़ंक्शन शून्य हो जाता है।

निर्देश

1. किसी फ़ंक्शन के शून्य का पता लगाने के लिए, आपको इसके दाहिने पक्ष को शून्य के बराबर करना होगा और परिणामी समीकरण को हल करना होगा। आइए कल्पना करें कि आपको एक फ़ंक्शन f(x)=x-5 दिया गया है।

2. इस फ़ंक्शन के शून्य को खोजने के लिए, आइए इसके दाहिने पक्ष को लें और शून्य के बराबर करें: x-5=0।

3. इस समीकरण को हल करने पर, हम पाते हैं कि x=5 और तर्क का यह मान फ़ंक्शन का शून्य होगा। अर्थात्, जब तर्क मान 5 है, तो फ़ंक्शन f(x) शून्य हो जाता है।

दृश्य के अंतर्गत कार्यगणित में हम समुच्चयों के तत्वों के बीच संबंध को समझते हैं। इसे और अधिक सही ढंग से कहें तो, यह एक "कानून" है जिसके अनुसार एक सेट का संपूर्ण तत्व (परिभाषा का डोमेन कहा जाता है) दूसरे सेट के एक निश्चित तत्व (मूल्यों का डोमेन कहा जाता है) से जुड़ा होता है।

आपको चाहिये होगा

• बीजगणित और गणितीय समीक्षा का ज्ञान।

निर्देश

1. मान कार्ययह एक निश्चित क्षेत्र है जहां से कोई फ़ंक्शन मान ले सकता है। आइए मानों की श्रेणी कहें कार्य f(x)=|x| 0 से अनंत तक. खोजने के लिए अर्थ कार्यएक निश्चित बिंदु पर आपको तर्क को प्रतिस्थापित करने की आवश्यकता होती है कार्यइसके संख्यात्मक समकक्ष, परिणामी संख्या होगी अर्थएम कार्य. मान लीजिए फलन f(x)=|x| – 10 + 4x. चलो पता करते हैं अर्थ कार्यबिंदु x=-2 पर. आइए x के स्थान पर संख्या -2 रखें: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. वह है अर्थ कार्यबिंदु -2 पर -16 के बराबर है।

टिप्पणी!
किसी बिंदु पर फ़ंक्शन का मान खोजने से पहले, सुनिश्चित करें कि यह फ़ंक्शन के डोमेन के भीतर है।

मददगार सलाह
एक समान विधि कई तर्कों के फ़ंक्शन के अर्थ की खोज करने की अनुमति देती है। अंतर यह है कि एक संख्या के बजाय आपको फ़ंक्शन के तर्कों की संख्या के अनुसार कई को प्रतिस्थापित करने की आवश्यकता होगी।

फ़ंक्शन वेरिएबल y और वेरिएबल x के बीच स्थापित कनेक्शन का प्रतिनिधित्व करता है। इसके अलावा, x के सभी मान, जिन्हें तर्क कहा जाता है, y - फ़ंक्शन के असाधारण मान के अनुरूप हैं। ग्राफ़िकल रूप में, एक फ़ंक्शन को ग्राफ़ के रूप में कार्टेशियन समन्वय प्रणाली पर दर्शाया जाता है। भुज अक्ष के साथ ग्राफ़ के प्रतिच्छेदन बिंदु, जिस पर तर्क x प्लॉट किए गए हैं, फ़ंक्शन के शून्य कहलाते हैं। स्वीकार्य शून्य ढूँढना किसी दिए गए फ़ंक्शन को खोजने के कार्यों में से एक है। इस मामले में, स्वतंत्र चर x के सभी अनुमेय मान जो फ़ंक्शन (डीओएफ) की परिभाषा का डोमेन बनाते हैं, को ध्यान में रखा जाता है।

निर्देश

1. किसी फ़ंक्शन का शून्य तर्क x का मान है जिस पर फ़ंक्शन का मान शून्य के बराबर होता है। हालाँकि, केवल वे तर्क जो अध्ययन के तहत फ़ंक्शन की परिभाषा के दायरे में हैं, शून्य हो सकते हैं। यानी ऐसे बहुत सारे मान हैं जिनके लिए फ़ंक्शन f(x) उपयोगी है।

2. दिए गए फ़ंक्शन को लिखें और इसे शून्य के बराबर करें, मान लें f(x) = 2x?+5x+2 = 0. परिणामी समीकरण को हल करें और इसकी वास्तविक जड़ें खोजें। विवेचक को खोजने के लिए द्विघात समीकरण के मूलों की गणना की जाती है। 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2, इस प्रकार, द्विघात समीकरण के संगत दो मूल प्राप्त होते हैं प्रारंभिक फ़ंक्शन f(x) के तर्क।

3. दिए गए फ़ंक्शन की परिभाषा के क्षेत्र से संबंधित सभी ज्ञात x मानों की जाँच करें। OOF का पता लगाएं, ऐसा करने के लिए, फॉर्म की सम जड़ों की उपस्थिति के लिए प्रारंभिक अभिव्यक्ति की जांच करें?f (x), हर में एक तर्क के साथ फ़ंक्शन में भिन्नों की उपस्थिति के लिए, लघुगणक या त्रिकोणमितीय की उपस्थिति के लिए भाव.

4. एक सम डिग्री की जड़ के तहत एक अभिव्यक्ति के साथ एक फ़ंक्शन पर विचार करते समय, सभी तर्क x को परिभाषा के क्षेत्र के रूप में लें, जिनके मान मूल अभिव्यक्ति को नकारात्मक संख्या में नहीं बदलते हैं (इसके विपरीत, फ़ंक्शन करता है) कोई मतलब नहीं)। जांचें कि फ़ंक्शन के ज्ञात शून्य स्वीकार्य x मानों की एक निश्चित सीमा के भीतर आते हैं या नहीं।

5. भिन्न का हर शून्य पर नहीं जा सकता, इसलिए उन तर्कों x को हटा दें जो ऐसे परिणाम की ओर ले जाते हैं; लघुगणकीय मात्राओं के लिए, तर्क के केवल उन मानों पर विचार किया जाना चाहिए जिनके लिए अभिव्यक्ति स्वयं शून्य से बड़ी है। फ़ंक्शन के शून्य जो सबलॉगरिदमिक अभिव्यक्ति को शून्य या ऋणात्मक संख्या में बदल देते हैं, उन्हें अंतिम परिणाम से हटा दिया जाना चाहिए।

टिप्पणी!
किसी समीकरण के मूल ज्ञात करते समय, अतिरिक्त मूल प्रकट हो सकते हैं। इसे जांचना आसान है: बस तर्क के परिणामी मान को फ़ंक्शन में प्रतिस्थापित करें और सुनिश्चित करें कि फ़ंक्शन शून्य हो गया है या नहीं।

मददगार सलाह
कभी-कभी कोई फ़ंक्शन अपने तर्क के माध्यम से स्पष्ट तरीके से व्यक्त नहीं होता है, तो यह जानना आसान है कि यह फ़ंक्शन क्या है। इसका एक उदाहरण एक वृत्त का समीकरण है.

जिसमें इसका मान शून्य हो जाता है। उदाहरण के लिए, सूत्र द्वारा दिए गए फ़ंक्शन के लिए

शून्य है क्योंकि

किसी फ़ंक्शन के शून्य भी कहलाते हैं फ़ंक्शन की जड़ें.

किसी फ़ंक्शन के शून्य की अवधारणा को किसी भी फ़ंक्शन के लिए माना जा सकता है जिसके मानों की श्रेणी में शून्य या संबंधित बीजगणितीय संरचना का शून्य तत्व होता है।

एक वास्तविक चर के फ़ंक्शन के लिए, शून्य वे मान हैं जिन पर फ़ंक्शन का ग्राफ़ x-अक्ष को काटता है।

किसी फ़ंक्शन के शून्य को खोजने के लिए अक्सर संख्यात्मक तरीकों (उदाहरण के लिए, न्यूटन की विधि, ग्रेडिएंट विधियां) के उपयोग की आवश्यकता होती है।

अनसुलझी गणितीय समस्याओं में से एक रीमैन ज़ेटा फ़ंक्शन के शून्य का पता लगाना है।

बहुपद का मूल

यह सभी देखें

साहित्य

विकिमीडिया फ़ाउंडेशन. 2010.

देखें अन्य शब्दकोशों में "फ़ंक्शन ज़ीरो" क्या है:

वह बिंदु जहां दिया गया फ़ंक्शन f(z) गायब हो जाता है; इस प्रकार, एन. एफ. f (z) समीकरण f (z) = 0 के मूल के समान है। उदाहरण के लिए, बिंदु 0, π, π, 2π, 2π,... फ़ंक्शन synz के शून्य हैं। एक विश्लेषणात्मक फ़ंक्शन के शून्य (विश्लेषणात्मक देखें... ...

शून्य कार्य, शून्य कार्य... वर्तनी शब्दकोश-संदर्भ पुस्तक

इस शब्द के अन्य अर्थ हैं, शून्य देखें। इस आलेख की सामग्री को "नल फ़ंक्शन" आलेख में ले जाना आवश्यक है। आप लेखों को संयोजित करके परियोजना में सहायता कर सकते हैं। यदि विलय की व्यवहार्यता पर चर्चा करना आवश्यक है, तो इसे बदलें... विकिपीडिया

या सी स्ट्रिंग (सी भाषा के नाम से) या एएससीआईजेड स्ट्रिंग (असेम्बलर निर्देश के नाम से) प्रोग्रामिंग भाषाओं में स्ट्रिंग्स का प्रतिनिधित्व करने की एक विधि, जिसमें एक विशेष स्ट्रिंग प्रकार पेश करने के बजाय, वर्णों की एक सरणी प्रयोग किया जाता है, और अंत में ... ...विकिपीडिया

क्वांटम क्षेत्र सिद्धांत में, युग्मन स्थिरांक के पुनर्सामान्यीकरण कारक को लुप्त करने की संपत्ति के लिए स्वीकृत (शब्दजाल) नाम वह है जहां जी0 इंटरेक्शन लैग्रेन्जियन, भौतिक से नंगे युग्मन स्थिरांक है। युग्मन स्थिरांक को अंतःक्रिया के रूप में प्रस्तुत किया जाता है। समानता Z... भौतिक विश्वकोश

शून्य उत्परिवर्तन एन-एलील- शून्य उत्परिवर्तन, एन. एलील * शून्य उत्परिवर्तन, एन। एलील * शून्य उत्परिवर्तन या एन। एलील या साइलेंट ए. एक उत्परिवर्तन जिसके कारण डीएनए अनुक्रम में कार्य पूरी तरह नष्ट हो जाता है जिसमें यह घटित हुआ... आनुवंशिकी। विश्वकोश शब्दकोश

संभाव्यता सिद्धांत में यह कथन कि कोई भी घटना (तथाकथित अवशिष्ट घटना), जिसकी घटना केवल स्वतंत्र यादृच्छिक घटनाओं या यादृच्छिक चर के अनुक्रम के मनमाने ढंग से दूर के तत्वों द्वारा निर्धारित की जाती है, ... ... गणितीय विश्वकोश

1) एक संख्या जिसमें यह गुण होता है कि कोई भी (वास्तविक या सम्मिश्र) संख्या उसमें जोड़ने पर नहीं बदलती। प्रतीक 0 द्वारा दर्शाया गया है। N द्वारा किसी भी संख्या का गुणनफल N के बराबर है।: यदि दो संख्याओं का गुणनफल N के बराबर है, तो कारकों में से एक ... गणितीय विश्वकोश

स्वतंत्र चर के बीच संबंधों द्वारा परिभाषित कार्य जो बाद वाले के सापेक्ष हल नहीं होते हैं; ये संबंध किसी फ़ंक्शन को निर्दिष्ट करने के तरीकों में से एक हैं। उदाहरण के लिए, संबंध x2 + y2 1 = 0 N.f को परिभाषित करता है। ... महान सोवियत विश्वकोश

2. फ़ंक्शन के शून्य ज्ञात कीजिए।

f(x) पर x .

x पर उत्तर f(x) दें .

2) x 2 >-4x-5;

एक्स 2 +4एक्स +5>0;

मान लीजिए f(x)=x 2 +4x +5 तो आइए ऐसा x खोजें जिसके लिए f(x)>0,

D=-4 कोई शून्य नहीं.

4. असमानताओं की व्यवस्था. दो चर वाली असमानताएँ और असमानताओं की प्रणालियाँ

1) असमानताओं की प्रणाली के समाधानों का समुच्चय उसमें शामिल असमानताओं के समाधानों के समुच्चय का प्रतिच्छेदन है।

2) असमानता f(x;y)>0 के समाधान के सेट को निर्देशांक तल पर ग्राफ़िक रूप से दर्शाया जा सकता है। आमतौर पर, समीकरण f(x;y) = 0 द्वारा परिभाषित रेखा विमान को 2 भागों में विभाजित करती है, जिनमें से एक असमानता का समाधान है। यह निर्धारित करने के लिए कि कौन सा भाग, आपको एक मनमाना बिंदु M(x0;y0) के निर्देशांक को प्रतिस्थापित करने की आवश्यकता है जो असमानता में रेखा f(x;y)=0 पर स्थित नहीं है। यदि f(x0;y0) > 0, तो असमानता का समाधान बिंदु M0 वाले विमान का हिस्सा है। यदि f(x0;y0)<0, то другая часть плоскости.

3) असमानताओं की प्रणाली के समाधानों का समुच्चय उसमें शामिल असमानताओं के समाधानों के समुच्चय का प्रतिच्छेदन है। उदाहरण के लिए, असमानताओं की एक प्रणाली दी जाए:

.

पहली असमानता के लिए, समाधानों का सेट त्रिज्या 2 का एक वृत्त है और मूल बिंदु पर केंद्रित है, और दूसरे के लिए, यह सीधी रेखा 2x+3y=0 के ऊपर स्थित एक अर्ध-तल है। इस प्रणाली के समाधानों का समुच्चय इन समुच्चयों का प्रतिच्छेदन है, अर्थात्। अर्धवृत्त.

4) उदाहरण. असमानताओं की प्रणाली को हल करें:

पहली असमानता का समाधान समुच्चय है, दूसरे का समुच्चय (2;7) और तीसरा समुच्चय है।

इन सेटों का प्रतिच्छेदन अंतराल (2;3] है, जो असमानताओं की प्रणाली के समाधान का सेट है।

5. अंतराल विधि का उपयोग करके तर्कसंगत असमानताओं को हल करना

अंतरालों की विधि द्विपद (x-a) के निम्नलिखित गुण पर आधारित है: बिंदु x = α संख्या अक्ष को दो भागों में विभाजित करता है - बिंदु α के दाईं ओर द्विपद (x-α)>0, और बिंदु α के बाईं ओर (x-α)<0.

असमानता को हल करना आवश्यक होने दें (x-α 1)(x-α 2)...(x-α n)>0, जहां α 1, α 2 ...α n-1, α n निश्चित हैं संख्याएँ, जिनके बीच कोई समान नहीं है, और ऐसी कि α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 अंतराल विधि का उपयोग करते हुए, निम्नानुसार आगे बढ़ें: संख्याएँ α 1, α 2 ...α n-1, α n संख्यात्मक अक्ष पर अंकित हैं; उनमें से सबसे बड़े के दाईं ओर के अंतराल में, यानी संख्याएँ α n, एक प्लस चिह्न लगाएं, इसके बाद दाएं से बाएं अंतराल में एक ऋण चिह्न लगाएं, फिर एक प्लस चिह्न, फिर एक ऋण चिह्न, आदि। फिर असमानता के सभी समाधानों का सेट (x-α 1)(x-α 2)...(x-α n)>0 उन सभी अंतरालों का मिलन होगा जिसमें प्लस चिह्न रखा गया है, और सेट असमानता के समाधान के (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) तर्कसंगत असमानताओं को हल करना (अर्थात् रूप की असमानताएँ P(x) Q(x) जहां बहुपद हैं) एक सतत फलन के निम्नलिखित गुण पर आधारित है: यदि एक सतत फलन बिंदु x1 और x2 (x1; x2) पर लुप्त हो जाता है और इन बिंदुओं के बीच कोई अन्य मूल नहीं है, तो में अंतराल (x1; x2) फ़ंक्शन अपना चिह्न बरकरार रखता है।

इसलिए, संख्या रेखा पर फ़ंक्शन y=f(x) के निरंतर चिह्न के अंतराल को खोजने के लिए, उन सभी बिंदुओं को चिह्नित करें जिन पर फ़ंक्शन f(x) गायब हो जाता है या असंततता से ग्रस्त हो जाता है। ये बिंदु संख्या रेखा को कई अंतरालों में विभाजित करते हैं, जिनमें से प्रत्येक के अंदर फ़ंक्शन f(x) निरंतर होता है और लुप्त नहीं होता है, अर्थात। चिह्न सहेजता है. इस चिह्न को निर्धारित करने के लिए, संख्या रेखा के विचारित अंतराल के किसी भी बिंदु पर फ़ंक्शन का चिह्न ढूंढना पर्याप्त है।

2) किसी परिमेय फलन के स्थिर चिह्न के अंतराल निर्धारित करना, अर्थात। एक तर्कसंगत असमानता को हल करने के लिए, हम संख्या रेखा पर अंश की जड़ों और हर की जड़ों को चिह्नित करते हैं, जो तर्कसंगत फ़ंक्शन की जड़ें और ब्रेकपॉइंट भी हैं।

अंतराल विधि का उपयोग करके असमानताओं को हल करना

3. < 20.

समाधान। स्वीकार्य मूल्यों की सीमा असमानताओं की प्रणाली द्वारा निर्धारित की जाती है:

फ़ंक्शन f(x) = के लिए – 20. f(x) खोजें:

जहां से x = 29 और x = 13.

एफ(30) = – 20 = 0.3 > 0,

एफ(5) = – 1 – 20 = – 10< 0.

उत्तर: । तर्कसंगत समीकरणों को हल करने की बुनियादी विधियाँ। 1) सबसे सरल: सामान्य सरलीकरणों द्वारा हल किया गया - एक सामान्य हर में कमी, समान पदों में कमी, और इसी तरह। द्विघात समीकरण ax2 + bx + c = 0 को हल किया जाता है...

X अंतराल पर बदलता है (0,1], और अंतराल पर घटता है)